力扣刷题笔记

好记性不如烂笔头

刷题trick

• 快慢指针的特性 ： 每轮移动之后两者的距离会加一

• 要有功能拆分的思想，不要总想着在一个函数内解题，而是应该想如何划分能够实现的部分（可以将这部分用单独函数实现，再在题解函数中调用），然后在这个基础上如何达到解题的目的，从易到难的过程

• 二叉树与路径相关的题目 要养成把路径题中的某个小功能进行拆解，然后在此基础上来不断往题目要求上靠

烂熟于心

变量声明

// 普通变量
int var = 1;
// 普通数组
int[] list = new int[length];
// 对象数据类型列表
List<Integer> objectList = new ArrayList<>();

数组

1. Java自带的对数组进行排序的方式

// 普通数据类型数组的内置排序方式：Arrays.sort()函数，默认升序排序
import java.util.Arrays;

int[] intArray = {5, 3, 8, 1, 2};
Arrays.sort(intArray);

// 对象类型 / 包装类型数组的排序方式：一样使用Arrays.sort()方法进行排序
Integer[] integerArray = {5, 3, 8, 1, 2};
Arrays.sort(integerArray);

// 集合类型数组 / 列表（ArrayList、Deque等）进行排序的方式
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;

List<Integer> integerList = new ArrayList<>();
Collections.sort(integerList);  // 通用（推荐，力扣能AC）

// Java8之后可以用内置的Sort()方法进行排序
integerList.sort(); // 不通用（不推荐！！！力扣会报错）

// 如果要降序排序，可以在排序函数中传入参数Comparator.reverseOrder()
import java.util.Comparator;

Arrays.sort(integerArray, Comparator.reverseOrder()); // 普通数组的降序排序
integerList.sort(Comparator.reverseOrder()); // 对象数组的降序排序
Collections.sort(integerList, Comparator.reverseOrder()); // 集合类型列表的降序排序，与上行写法不太一致

2. 普通数据类型数组和对象类型数组之间的转换

链表

1. 插入和删除节点的写法
2. 计算中间节点的写法（中间靠前节点和中间靠后节点都要会写）

二叉树

1. 二叉树的三种递归遍历和迭代遍历、层序遍历

中序遍历是借助栈来实现的

1. 递归算深度、递归算直径

查找

【二分查找的模板】

nums是非递减的数组

用闭区间写法，就是初始左右边界的赋值，分别是数组两边的下标索引，即0和nums.lnegth-1

// 闭区间写法
public int binarySearch(int[] nums, int target) {
    int left = 0, right = nums.length - 1;

    while (left <= right) {
        int mid = (right - left) / 2 + left; // 这样写避免相加导致内存泄漏
        if (target == nums[mid]) {
            return mid;
        else if (target < nums[mid]) {
            right = mid - 1;
        } else {
            left = mid + 1;
        }
    }

    return left; // 返回需要插入的位置索引
}

// 返回最小满足nums[i] >= target的下标i
// 如果数组为空，或者所有数都 < target，则返回 nums.length
// 要求 nums 是非递减的，即 nums[i] <= nums[i + 1]
public int binarySearch(int[] nums, int target) {
    int left = 0, right = nums.length - 1;

    while (left <= right) {
        int mid = (right - left) / 2 + left;
        // 注意这里的判断条件
        if (target <= nums[mid]) {
            right = mid - 1;
        } else {
            left = mid + 1;
        }
    }

    return left;  // 最后返回left，即是最小满足nums[i]>=target的位置坐标，target应该插入这个位置
}

【寻找旋转数组中的最小值】

数组不包含重复值

旋转后的数组如下图所示，肯定分为两段，前半段升序和后半段升序

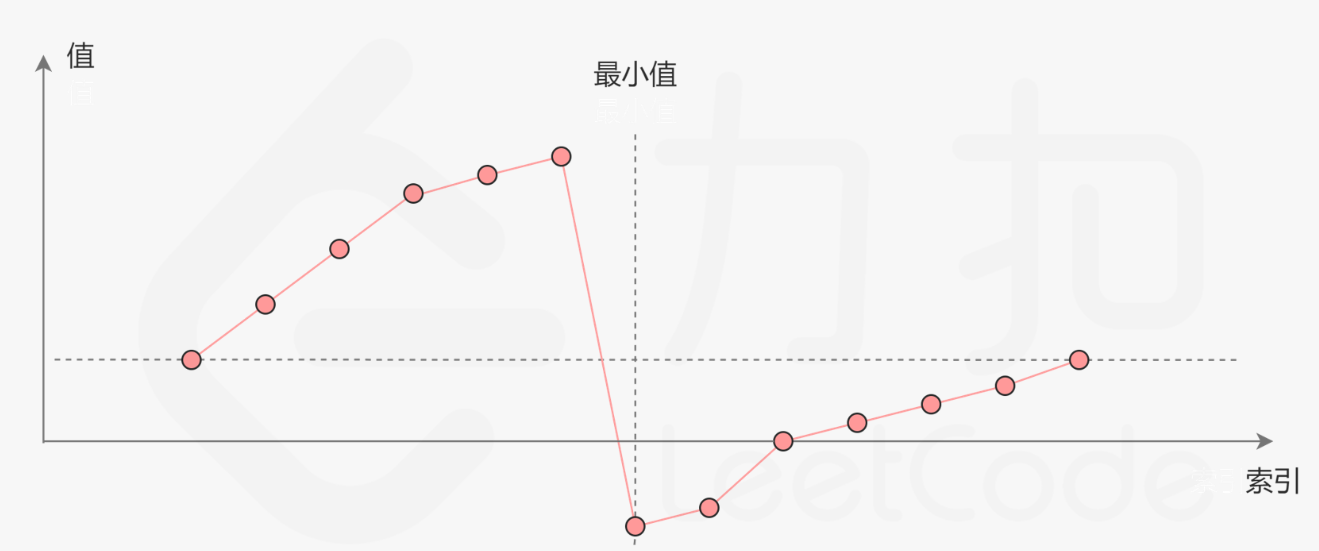
旋转后的数组一定被分成了前后两部分且两半都是升序数组，且前一半的最小值一定大于后一半的最大值，只要用二分找到后一半的第一个元素即可

只需要考虑mid是在前半段升序（nums[mid] > nums[right]）还是在后半段升序（nums[mid]<nums[right]） 中

mid在后半段升序的话，最小值肯定在mid左边，因此设：right=mid；

mid在前半段的话，最小值肯定在mid的右边，因此设：left=mid+1；

27. 移除元素

题目描述

给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素，并返回移除后数组的新长度。

不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并 原地 修改输入数组。

元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

题解

暴力解法：

// 时间复杂度：O(n^2)
// 空间复杂度：O(1)
class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        int size = nums.size();
        for (int i = 0; i < size; i++) {
            if (nums[i] == val) { // 发现需要移除的元素，就将数组集体向前移动一位
                for (int j = i + 1; j < size; j++) {
                    nums[j - 1] = nums[j];
                }
                i--; // 因为下标i以后的数值都向前移动了一位，所以i也向前移动一位
                size--; // 此时数组的大小-1
            }
        }
        return size;
    }
};

双指针：

//时间复杂度：O(n^2)
//空间复杂度：O(1)
//元素的相对位置没有发生改变
class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        int slowIndex = 0;  //慢指针指向
        for (int fastIndex = 0; fastIndex < nums.size(); fastIndex++) {
            //当fastIndex指向val时，慢指针不动
            if (nums[fastIndex] != val) {  //当没找到val时，将快指针所指向的值nums[fastIndex]赋值给此时慢指针所指向的值nums[slowIndex]，因此此时慢指针指向的值一定是val。赋值即使移除值为val的元素。
                nums[slowIndex++] = nums[fastIndex];  //slowIndex++是为了保证当赋值发生时，慢指针也得往下走，因为当前slowIndex被赋值后肯定不是val了，slowIndex总是指向val所在的位置
            }
        }
        return slowIndex;
    }
};

例如：nums：2 3 3 4 8 3 9 1 val：3

快排式双指针法：

/**
* 相向双指针方法，基于元素顺序可以改变的题目描述改变了元素相对位置，确保了移动最少元素
* 时间复杂度：O(n)
* 空间复杂度：O(1)
*/
class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        int leftIndex = 0;
        int rightIndex = nums.size() - 1;
        while (leftIndex <= rightIndex) {
            // 找左边等于val的元素
            while (leftIndex <= rightIndex && nums[leftIndex] != val){
                ++leftIndex;
            }
            // 找右边不等于val的元素
            while (leftIndex <= rightIndex && nums[rightIndex] == val) {
                -- rightIndex;
            }
            // 将右边不等于val的元素覆盖左边等于val的元素
            if (leftIndex < rightIndex) {
                nums[leftIndex++] = nums[rightIndex--];    //自加表示在新的元素区间(去除刚才检查过的)重新执行判断
            }
        }
        //循环执行结束的时候，leftIndex右边不为val的元素全部都赋值到leftIndex左边，因此leftIndex即为移除后数组长度
        return leftIndex;   // leftIndex一定指向了最终数组末尾的下一个元素
    }
};

注意：左指针用来找到元素值为val的元素，因此再循环里需要用nums[leftIndex]!=val，这样停止循环的时候就找到了值为val的元素

右指针用来找到元素值不是val的元素，因此循环里判断需要写nums[rightIndex]==val，同上原理

977. 有序数组的平方

题目描述

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

示例 1：

输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]

示例 2：

输入：nums = [-7,-3,2,3,11]
输出：[4,9,9,49,121]

提示：

• 1 <= nums.length <= 104
• -104 <= nums[i] <= 104
• nums 已按 非递减顺序 排序

题解

暴力解法：先平方再排序

//时间复杂度O(n+nlogn)，快速排序
class Solution {
public:
    vector<int> sortedSquares(vector<int>& nums) {
        //先对元素都平方
        for (int i = 0; i < nums.size(); i++) {
            nums[i] *= nums[i];
        }
        //对nums进行快速排序
        quickSort(nums, 0, nums.size() - 1);
    }
    //划分函数
    int Partition(vector<int>& nums, int low, int high) {
        int pivot = nums[high];
        int i = low - 1;
        for (int j = low; j < high; j++) {
            if (nums[j] <= pivot) {
                i++;
                int temp1 = nums[i];
                nums[i] = nums[j];
                nums[j] = temp1;
            }
        }
        int temp2 = nums[i + 1];
        nums[i + 1] = nums[high];
        nums[high] = temp2;
    }

    //快速排序算法
    void quickSort(vector<int>& nums, int low, int high) {
        if (low < high) {
            int partitionIndex = Partition(nums, low, high);
            quickSort(nums, low, partitionIndex - 1);
            quickSort(nums, partitionIndex + 1, high);
        }
    }
};

双指针解法

class Solution {
public:
    vector<int> sortedSquares(vector<int>& A) {
        int k = A.size() - 1;  //指向result数组末尾的指针
        vector<int> result(A.size(), 0);
        for (int i = 0, j = A.size() - 1; i <= j;) { // 注意这里要i <= j，因为最后要处理两个元素
            if (A[i] * A[i] < A[j] * A[j])  {
                result[k--] = A[j] * A[j];
                j--;
            }
            else {
                result[k--] = A[i] * A[i];
                i++;
            }
        }
        return result;
    }
};

209. 长度最小的子数组【经典】

题目描述

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度**。**如果不存在符合条件的子数组，返回 0 。

示例 1：

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：

输入：target = 4, nums = [1,4,4]
输出：1

示例 3：

输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

提示：

• 1 <= target <= 109
• 1 <= nums.length <= 105
• 1 <= nums[i] <= 105

题解

暴力解法

// 时间复杂度O(n^2)
// 存在一些测试用例超出时长限制
class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        // 暴力解法
        int result = INT32_MAX;
        int sum = 0;  // 子序列总和
        int subLength = 0;  //计算子序列长度
        for (int i = 0; i < nums.size(); i++) {
            sum = 0;
            for (int j = i; j < nums.size(); j++) {
                sum += nums[j];        // 先累加在进行判断
                subLength = j - i + 1; //关键，计算子序列的长度
                if (sum >= target) {
                    result = result < subLength ? result : subLength;  // 条件运算符来判断是否更新result
                }
            }
        }
        return result == INT32_MAX ? 0 : result;
    }
};